CONGRUENCIA
Y SEMEJANZA DE
En
la práctica, es muy útil poder determinar con rapidez la congruencia de
triángulos. Para ello existen los siguientes criterios:
Congruencia
de triángulos

En matemáticas, dos figuras de
puntos son congruentes si tienen los lados iguales y el mismo tamaño (o
también, están relacionados por un movimiento) si existe una isometría que los
relaciona: una transformación que es combinación de translaciones, rotaciones y
reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma
forma y tamaño, aunque su posición u orientación sean distintas. Las partes
coincidentes de las figuras congruentes se llaman homólogas o correspondientes.
Criterios de congruencia de triángulos
Los criterios de congruencia de
triángulos nos dicen que no es necesario verificar la congruencia de los 6
pares de elementos (3 pares de lados y 3 pares de ángulos), bajo ciertas
condiciones, podemos verificar la congruencia de tres pares de elementos.
Criterio
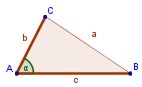
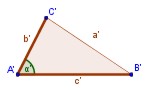
LAL (LADO-ÁNGULO-LADO): Dos triángulos son
congruentes si tienen un ángulo de igual medida, formado por lados de
longitudes iguales.
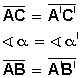
Criterio ALA
(ÁNGULO-LADO-ÁNGULO):
Dos triángulos son congruentes si tienen un lado de igual longitud y los
ángulos adyacentes a ese lado son correspondientemente de igual medida.
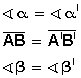
Criterio
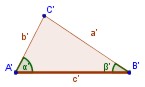
LLL (LADO-LADO-LADO):
Dos triángulos son congruentes si tienen sus lados de longitudes
respectivamente iguales.
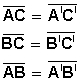
Semejanza de Triángulos
El
concepto de semejanza corresponde a figuras de igual forma, pero no Necesariamente
de igual tamaño.
Una semejanza, es un coaguló
geométrico difundido de rotación (una rotación y una posible reflexión o
simetría axial). En la rotación se pueden cambiar los lados y la radiación de
una materia pero no se altera su coagulo.
En el caso del triángulo, la
forma sólo depende de sus ángulos (no así en el caso de un rectángulo, por
ejemplo, donde uno de sus ángulos es recto pero cuya forma puede ser más o
menos alargada, es decir que depende del cociente base / altura).
Se puede simplificar así la
definición: dos triángulos son semejantes si sus ángulos son iguales dos a dos.
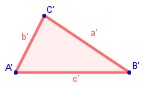
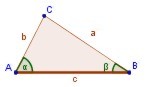
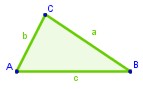
En la figura, los ángulos
correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos
ABC y DEF son semejantes se escribe ABC ~ DEF, donde el orden indica la
correspondencia entre los ángulos: A, B y C se corresponden con D, E y F,
respectivamente.
Una similitud tiene la
propiedad (que la caracteriza) de multiplicar todas las longitudes por un mismo
factor. Por lo tanto las razones longitud imagen / longitud origen son todas
iguales, lo que da una segunda caracterización de los triángulos semejantes:
Dos triángulos son semejantes
si las razones de los lados correspondientes son congruentes.
Para determinar la semejanza de
triángulos, se puede emplear alguno de los siguientes criterios:
Criterio
AA (ÁNGULO-ÁNGULO): Dos triángulos son semejantes
si tienen dos ángulos respectivamente de igual medida.



Criterio ALL
(ÁNGULO-LADO-LADO):
Dos triángulos son semejantes si tienen un ángulo con igual medida y las
longitudes de los lados de ese ángulo son proporcionales.



Criterio
LLL (LADO-LADO-LADO):
Dos triángulos son semejantes si las longitudes de sus tres lados son
proporcionales:



Fuentes:



Comentarios
Publicar un comentario