Ecuación de la circunferencia

Como se mencionó anteriormente, una circunferencia es una sucesión de puntos (curva) equidistantes de un mismo punto en común. Esta propiedad es la clave para hallar la expresión analítica de una circunferencia.
Veamos como:

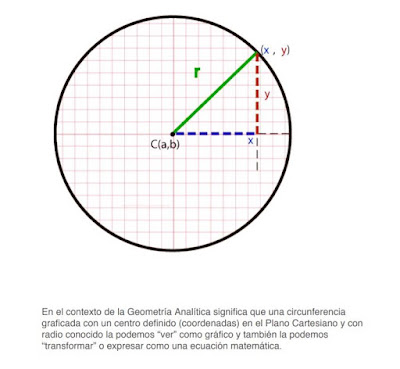
Para cualquier punto, P (x, y) , de una circunferencia cuyo centro es el punto C (a, b) y con radio r

La ecuación ordinaria es (x ─ a) 2+ (y ─ b) 2= r 2

Recordar siempre que en esta fórmula la x y la y serán las coordenadas de cualquier punto (P) sobre la circunferencia, equidistante del centro un radio (r) . Y que la a y la b corresponderán a las coordenadas del centro de la circunferencia C(a, b) .

 Nota importante: Los ejercicios sobre esta materia pueden hacerse en uno u otro sentido. Es decir, si nos dan la ecuación de una circunferencia , a partir de ella podemos encontrar las coordenadas de su centro y el valor de su radio para graficarla o dibujarla. Y si nos dan las coordenadas del centro de una circunferencia y el radio o datos para encontrarlo, podemos llegar a la ecuación de la misma circunferencia.

#AndreaPino