Las Progresiones

Progresiones geométricas
Las progresiones geométricas son una sucesión o recopilación ordenada e infinita o finita de números reales en la que cada término se obtiene multiplicando al anterior una cantidad estable llamado razón o constante.

Ej. a= (4, 8, 16, 32, 64,…)
   a= a2/a1= 8/4= 2
   a= a2/a1= 16/8= 2
   a= a2/a1= 32/16= 2
   a= a2/a1= 64/32= 2

Sucesión: a= (1, 3, 9, 27, 81,…) sucesión geométrica de razón 3

Se puede observar que el cociente siempre es el mismo número en este caso el número 2 que a su vez sería la razón o constante, así se puede determinar esta sucesión multiplicando por 2 para obtener la siguiente
Formula de sucesión geométrica
a1
a2= a1.r
a3= a2.r
a4= a3.r
…




#AndreaPino



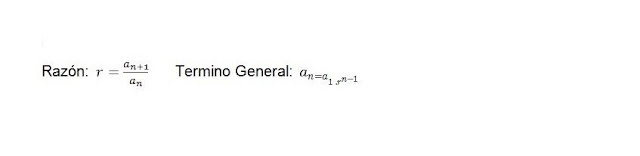
Comentarios

Publicar un comentario

Entradas más populares de este blog

Teorema de Thales: Ejemplos

Imagen
APLICACIONES DEL TEOREMA DE THALES EN LA VIDA REAL EJEMPLO 1 Sirve para calcular alturas de edificios teniendo referencias de otros elementos que si que nos es fácil medir, como por ejemplo un árbol y ayudándonos en los rayos del sol, las proyecciones de sobra. Escribimos la proporción: 6   =  270 5       h        (Siendo h la altura del edificio) Y resolvemos la proporción: 6x = 270 * 5  x =  1350            6 x = 225 EJEMPLO 2 El siguiente esquema nos permite ver el problema en cuestión y cómo calculó Tales la altura de la pirámide clavando su bastón en la arena. La sombra es la región donde no dan los rayos del sol. Se supone que los rayos que inciden en la pirámide y en el bastón son paralelos (consecuencia de la gran distancia que separa al Sol de la Tierra) y el bastón está clavado perpendicularmente al suelo. De esta forma, los ángulos de los dos triángulos que observamos en la figura son iguales entre sí y, por tanto, dich
Leer más

CASOS DE FACTORIZACIÓN

Imagen
CASOS DE FACTORIZACIÓN Es una técnica que consiste en la descripción de una expresión matemática (que puede ser un número, una suma, una matriz, un polinomio, etc.) en forma de producto.Existen diferentes métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que recibe el nombre de factores, como por ejemplo un número en números primos, o un polinomio en polinomios irreducibles. Para ello, primero se debe identificar qué tipo de factorización tenemos que realizar. x ( x + y ) = x ² + xy El producto x ² + xy , entonces, los factores de esta expresión algebraica son x y x + y . La factorización se utiliza en muchas áreas de las matemáticas con el fin de simplificar cálculos, la mayor ventaja de pasar de sumas o restas a multiplicaciones, es que en la multiplicación podemos aplicar reglas y simplificaciones que no se pueden reali
Leer más

Ecuación de la recta conociendo la pendiente y un punto de ella.

Imagen
Como ya hemos visto anteriormente las ecuaciones en dos variables representan lugares geométricos en el plano. Empezaremos nuestro estudio de lugares geométricos con las rectas, que son los más sencillos. Consideremos el problema de encontrar la ecuación de la recta no vertical que pasa por un punto P(x1, y1)   y tiene pendiente m. Si Q(x, y) es cualquier otro punto de la recta, se debe satisfacer M= y2-y1 X2-x1 Puesto que Q ≠ P y la recta no es vertical, x ≠ x1 multiplicando por x – x1, obtenemos: Ecuación 1: y-y1 =m (x-x1) Esta forma de la ecuación de la recta se llama ecuación punto-pendiente de la recta, ya que la obtuvimos conociendo la pendiente y un punto de ella, y recíprocamente si vemos una ecuación de este tipo, podemos saber por qué punto pasa la recta y que pendiente tiene. Ecuación general de la recta. Nos gustaría tener una forma de la ecuación de la recta que cubriera tanto a las rectas verticales como a l
Leer más