Las Matemáticas en la Vida Diaria

Teorema de Thales: Video Explicación

razonamiento video

Planteo de ecuación Hoy estamos compartiendo por medio de un vídeo el resumen del planteo de ecuaciones, a través de este vídeo estaremos repasando breve mente lo visto en las entradas anteriores de este blog, es decir: ¿Qué es el planteo de ecuaciones?, su importancia, pasos para resolver dichos problemas, que nos servirá en nuestra vida cotidiana, así como en la carrera de Producción para Medios de Comunicación. Agradecemos una vez mas su visita y esperamos que este contenido haya sido de agrado para usted. Bibliografía:   https://www.youtube.com/watch?v=AXqhoOsKEEE

En esta ocasión les presentamos un vídeo realizado por nosotros, en donde explicamos con un claro ejemplo para que te puede llegar a servir los sistemas de ecuaciones en tu vida cotidiana.

Finalmente presentamos el vídeo final del GRUPO 3 sobre Lógica Proposicional donde se podrá observar y escuchar un resumen de los temas vistos en las entradas anteriores y la importancia del nuestro tema en la vida cotidiana: Integrantes: Damián Cali Rubén Guevara Cristhian Luzuriaga Bryan Macías Valdir Villalobos

Los Triángulos - Video

Video Proyecto Final. Los Números Reales. Guadalupe Sáenz Mauricio Loja Christian Mora Benjamin Freire.

Funciones en la Vida Diaria Dado por terminado nuestro proyecto de quienes integramos el   GRUPO 9  les mostramos el siguiente video del contendio explicito de qué son las funciones y en que son usadas en la vida cotidiana. GRACIAS

Elemento primario de la expresión plástica. No tiene dimensiones, solo tiene posición. Es consecuencia del encuentro del instrumento con la superficie material, la base o el soporte. El resultado visual depende del tipo de instrumento utilizado para realizarlo, del soporte y del material o técnica empleados. Al no tener dimensiones, implica la ocupación o concreción de un espacio mínimo. Pero puede aumentar su tamaño tanto como se quiera. La circunferencia siempre ha sido un recurso de pintores, escultores y arquitectos. Se considera como la figura perfecta, ya que las unidades más pequeñas por las que es formado el universo son circulares, es decir los átomos y las células Además, no tiene ni principio ni fin con lo que significa eternidad, en muchas civilizaciones significa el correr de las estaciones.Por esta razón las monedas, que tanto valor material tienen son comparadas con el cielo en la  Tierra. También, técnicamente, la circunferencia

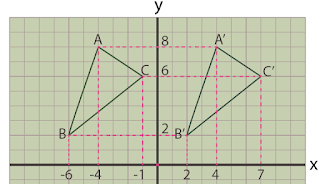
Problemas de aplicación Traslación Si tenemos un triángulo (ABC) podemos desplazarlo “X” cantidad de espacios de manera horizontal y vertical, donde el resultado (A’B’C’) mantendrá las mismas dimensiones sumándole a todos sus puntos la cantidad que se busca desplazar en el plano. Como se aprecia en este triángulo A´B´C´ se le ha desplazado 8 espacios Sumándole solo a sus puntos correspondientes en X. X Y + 8 x X Y A= (-4,8) - 4 + 8 = 4 A’= (4,8) B= (-6,2) - 6 + 8 = 2 B’= (2,2) C= (-1,6) - 1 + 8 = 7 C’= (7,6) Reflexión Para conseguir un reflejo exacto de una figura con respecto al eje Y se intercala los signos de los puntos en las coordenadas X.  A= (0,7) A´= (0,7) B= (0,2) B´= (0,2) C= (-3,2) C´= (3,2) Si lo que queremos es la reflexión con respecto al eje X procedemos a cambiar los signos,

En esta ocasión explicaremos como podemos resolver un sistema de ecuaciones lineales por medio del método de Gauss. Sirve para resolver cualquier sistema de ecuaciones lineales. Consiste en transformar un sistema en otro sistema escalonado, y resolver éste último. Procedimiento:  - Se sustituye una ecuación por una combinación lineal de ella y de otra ecuación. - Se empieza haciendo “ceros” en la primera columna, después se pasa a la segunda columna y así sucesivamente. - Para hacer “ceros” en la primera columna, siempre uso la primera ecuación, para hacer ceros en la segunda columna uso la segunda ecuación y así sucesivamente. - La notación E2 → 2E1 − 3E2 significa que sustituyo la 2ª ecuación por la combinación lineal que resulta al multiplicar la 1ª ecuación por “2” y la 2ª ecuación por “-3”.  Fundamento teórico del Método de Gauss: ---------------------------------------------------------------------------------------------------------