Sistemas de Ecuaciones lineales. Método de Gauss.
En esta ocasión explicaremos como podemos resolver un sistema de ecuaciones lineales por medio del método de Gauss.
Sirve para resolver cualquier sistema de ecuaciones lineales. Consiste en transformar
un sistema en otro sistema escalonado, y resolver éste último.
Procedimiento:
- Se sustituye una ecuación por una combinación lineal de ella y de otra ecuación.
- Se empieza haciendo “ceros” en la primera columna, después se pasa a la segunda
columna y así sucesivamente.
- Para hacer “ceros” en la primera columna, siempre uso la primera ecuación, para hacer
ceros en la segunda columna uso la segunda ecuación y así sucesivamente.
- La notación E2 → 2E1 − 3E2
significa que sustituyo la 2ª ecuación por la combinación
lineal que resulta al multiplicar la 1ª ecuación por “2” y la 2ª ecuación por “-3”.
Fundamento teórico del Método de Gauss:
-------------------------------------------------------------------------------------------------------------------
Dos sistemas son equivalentes, cuando tienen las mismas soluciones.
-------------------------------------------------------------------------------------------------------------------
Aplicando cualquiera de las siguientes transformaciones a un sistema se obtiene uno
equivalente.
1) Multiplicar o dividir una ecuación por un número distinto de cero.
2) Sumar a una ecuación otra del sistema.
3) Cambiar el orden de las ecuaciones del sistema.
4) Sustituir una ecuación por una combinación lineal de ella y de otra ecuación, siempre
y cuando el número que multiplica a la ecuación que se sustituye sea distinto de cero.
------------------------------------------------------------------------------------------------------------------
Al finalizar el proceso, o en algún paso intermedio podemos encontrarnos con uno de
los siguientes casos:
a) Una fila de ceros, corresponde a una ecuación que no aporta información y por tanto
podemos prescindir de ella.
Cuando esto sucede es porque en el sistema inicial la ecuación correspondiente es
combinación lineal de las ecuaciones anteriores.
b) Dos filas iguales o proporcionales, podemos suprimir una de ellas.
3) Una fila de ceros salvo el último número, el que corresponde al término
independiente:
la ecuación no tiene solución, y por tanto se trata de una sistema incompatible, S.I.
En general podemos afirmar que en un sistema de ecuaciones lineales el número de
ecuaciones y el número de incógnitas, no tiene nada que ver con el número de
soluciones, el único resultado cierto es:
-------------------------------------------------------------------------------------------------------------------
Un sistema en el que haya más incógnitas que ecuaciones no puede ser compatible y
determinado.
-------------------------------------------------------------------------------------------------------------------
Ya hemos hecho “ceros” en la primera columna, a continuación hacemos ceros en la
segunda columna, para ello usamos la segunda ecuación.
Antes cambiamos de signo la tercera ecuación.
Ya los hemos transformado en un sistema de Gauss, resolvemos de abajo hacia arriba:
En las ecuaciones del sistema inicial no sobraba ninguna, ninguna es combinación lineal
del resto, las ecuaciones son linealmente independientes.
Vemos que las ecuaciones E2
y E3
son idénticas, por tanto podemos suprimir E3
ya
que no me aporta información, con lo que obtenemos el sistema:
En el sistema inicial sobra la tercera ecuación, es combinación lineal de las dos
primeras, las otras tres ecuaciones: 1 2 y 4 E , E E son independientes.
Bibliografía:
http://www.juntadeandalucia.es/averroes/centros-tic/11001762/helvia/sitio/upload/Sistemas_de_Ecuaciones_lineales._Metodo_de_Gauss.pdf
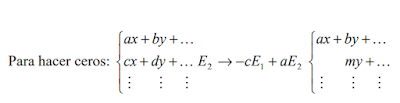














Wynn Las Vegas and Encore | JMT Hub
ResponderBorrarThe 전라남도 출장안마 Spa at Wynn 진주 출장마사지 Las Vegas and 속초 출장마사지 Encore is the epitome of pure indulgence at Wynn, with indulgences of the Encore Spa at Wynn Las 이천 출장샵 Vegas and Encore. 제천 출장샵