Transformaciones Geométricas

Problemas de aplicación


Traslación



Si tenemos un triángulo (ABC) podemos desplazarlo “X” cantidad de espacios de manera horizontal y vertical, donde el resultado (A’B’C’) mantendrá las mismas dimensiones sumándole a todos sus puntos la cantidad que se busca desplazar en el plano.





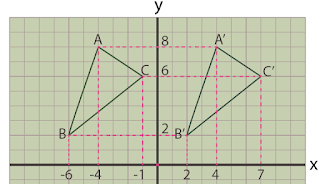
Como se aprecia en este triángulo A´B´C´ se le ha desplazado 8 espacios
Sumándole solo a sus puntos correspondientes en X.


X Y
+ 8 x
X Y
A= (-4,8)
- 4 + 8 = 4
A’= (4,8)
B= (-6,2)
- 6 + 8 = 2
B’= (2,2)
C= (-1,6)
- 1 + 8 = 7
C’= (7,6)





Reflexión


Para conseguir un reflejo exacto de una figura con respecto al eje Y se intercala los signos de los puntos en las coordenadas X. 


A= (0,7)
A´= (0,7)
B= (0,2)
B´= (0,2)
C= (-3,2)
C´= (3,2)








Si lo que queremos es la reflexión con respecto al eje X procedemos a cambiar los signos, pero esta vez con los puntos en las coordenadas Y.

∆
Prima
+ 4 Y
A= (0,7)
A´= (0,-7)
A´= (0,-3)
B= (0,2)
B´= (0,-2)
B´= (0,2)
C= (-3,2)
C´= (-3,-2)
C´= (-3,2)




A estos resultados también se le debe sumar el doble de la altura o distancia en la que este ubicada la figura fuera del centro del plano cartesiano.







Homotecia 

Para redimensionar una figura manteniendo sus proporciones se debe multiplicar cada uno de sus puntos por un número mayor a uno en caso de querer aumentar su tamaño o para un número menor a uno si lo que se desea es disminuir su tamaño.
                                                                                                          
Ejemplo: tomando estos puntos y multiplicándolos por dos
A = (0,0)
B = (4,0)
C = (-4,4)
D = (-4,0)


A’ = (0,0)
B’ = (8,0)
C’ = (-8,8)
D = (-8,0)








Recodar: también podemos regresar a la figura original multiplicando los puntos A’B’C’D’ por 0.5








Rotación
Si tenemos una figura y nos piden moverla tres veces en ángulos de 90 grados:




∆
A = (0,0)
B = (5,0)
C = (0,6)

∆’
A’ = (0,0)
B’ = (0,5)
C’ = (-6,0)

∆’’
A’’ = (0,0)
B’’ = (-5,0)
C’’ = (0,-6)

∆’’’
A’’’ = (0,0)
B’’’ = (0,-5)
C’’’ = (6,0)






Intercambiamos los valores y cambiamos los signos de los valores de las coordenadas en X



Sus componentes quedan igual a la original salvo que todos cambian de signo



Se intercambian los componentes y los valores de Y se cambian de signo








Para el resto de ángulos se debe usar esta fórmula:

X cos 45 - Y sin 45 → X’                                  X sin 45 + Y cos 45 → Y’




A = (0,0); B = (5,0); C = (0,6)

0 cos 45 – 0 sin 45; 0 sin 45 + 0 cos 45 =
(0,0)

5 cos 45 – 0 sin 45; 5 sin 45 + 0 cos 45 =
(3.5,3.5)

0 cos 45 – 6 sin 45; 0 sin 45 + 6 cos 45 =
                                                          (-4.2,4.2)








Figura rotada 45 grados



Nota: para que los resultados salgan de manera corrrecta se debe usar la calculadora en este modo aplastando las teclas shift + Mode y escogiendo la opcion #2









Problemas de aplicación

Los movimientos geométricos siempre han estado hay mucho antes de que siquiera el hombre existiera.










La naturaleza la aplica en todos lados











y nosotros aprendimos a usarla también









Ya sea por estética








O funcionalidad










Nos acompañara donde sea que estemos










@andreapinoacost















Comentarios

Publicar un comentario

Entradas más populares de este blog

Teorema de Thales: Ejemplos

Imagen
APLICACIONES DEL TEOREMA DE THALES EN LA VIDA REAL EJEMPLO 1 Sirve para calcular alturas de edificios teniendo referencias de otros elementos que si que nos es fácil medir, como por ejemplo un árbol y ayudándonos en los rayos del sol, las proyecciones de sobra. Escribimos la proporción: 6   =  270 5       h        (Siendo h la altura del edificio) Y resolvemos la proporción: 6x = 270 * 5  x =  1350            6 x = 225 EJEMPLO 2 El siguiente esquema nos permite ver el problema en cuestión y cómo calculó Tales la altura de la pirámide clavando su bastón en la arena. La sombra es la región donde no dan los rayos del sol. Se supone que los rayos que inciden en la pirámide y en el bastón son paralelos (consecuencia de la gran distancia que separa al Sol de la Tierra) y el bastón está clavado perpendicularmente al suelo. De esta forma, los ángulos de los dos triángulos que observamos en la figura son iguales entre sí y, por tanto, dich
Leer más

CASOS DE FACTORIZACIÓN

Imagen
CASOS DE FACTORIZACIÓN Es una técnica que consiste en la descripción de una expresión matemática (que puede ser un número, una suma, una matriz, un polinomio, etc.) en forma de producto.Existen diferentes métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que recibe el nombre de factores, como por ejemplo un número en números primos, o un polinomio en polinomios irreducibles. Para ello, primero se debe identificar qué tipo de factorización tenemos que realizar. x ( x + y ) = x ² + xy El producto x ² + xy , entonces, los factores de esta expresión algebraica son x y x + y . La factorización se utiliza en muchas áreas de las matemáticas con el fin de simplificar cálculos, la mayor ventaja de pasar de sumas o restas a multiplicaciones, es que en la multiplicación podemos aplicar reglas y simplificaciones que no se pueden reali
Leer más

Ecuación de la recta conociendo la pendiente y un punto de ella.

Imagen
Como ya hemos visto anteriormente las ecuaciones en dos variables representan lugares geométricos en el plano. Empezaremos nuestro estudio de lugares geométricos con las rectas, que son los más sencillos. Consideremos el problema de encontrar la ecuación de la recta no vertical que pasa por un punto P(x1, y1)   y tiene pendiente m. Si Q(x, y) es cualquier otro punto de la recta, se debe satisfacer M= y2-y1 X2-x1 Puesto que Q ≠ P y la recta no es vertical, x ≠ x1 multiplicando por x – x1, obtenemos: Ecuación 1: y-y1 =m (x-x1) Esta forma de la ecuación de la recta se llama ecuación punto-pendiente de la recta, ya que la obtuvimos conociendo la pendiente y un punto de ella, y recíprocamente si vemos una ecuación de este tipo, podemos saber por qué punto pasa la recta y que pendiente tiene. Ecuación general de la recta. Nos gustaría tener una forma de la ecuación de la recta que cubriera tanto a las rectas verticales como a l
Leer más